Métodos tabulares y gráficos
La distribución de frecuencias es la forma en la que un
conjunto de datos se clasifica en distintos grupos excluyentes entre sí. Es
decir, si un dato pertenece a un grupo no puede pertenecer a otro.
También es la manera en
la que se ordena una serie de observaciones en diferentes grupos, y normalmente
en modo ascendente o descendente.
Las distribuciones de frecuencias son tablas en que se dispone las modalidades de la variable por filas. En las columnas se dispone el número de ocurrencias de cada valor, porcentajes, etc.
La finalidad de las agrupaciones en frecuencias es facilitar la obtención de la información que contienen los datos.
La distribución de frecuencias es la forma en la que un
conjunto de datos se clasifica en distintos grupos excluyentes entre sí. Es
decir, si un dato pertenece a un grupo no puede pertenecer a otro.
También es la manera en
la que se ordena una serie de observaciones en diferentes grupos, y normalmente
en modo ascendente o descendente.
Las distribuciones de frecuencias son tablas en que se dispone las modalidades de la variable por filas. En las columnas se dispone el número de ocurrencias de cada valor, porcentajes, etc.
La finalidad de las agrupaciones en frecuencias es facilitar la obtención de la información que contienen los datos.
Tipos de distribuciones de frecuencia:
- · Frecuencia absoluta(fi): Es la cantidad de observaciones que pertenecen a cada grupo. También,
se interpreta como la cantidad de veces que se repite un suceso.
- · Frecuencia relativa(hi): Se calcula dividiendo la frecuencia absoluta entre el número de datos.
- · Frecuencia absoluta acumulada(Fi): Resulta de sumar las frecuencias
absolutas de una clase o grupo de la muestra (o población) con la anterior o
las anteriores.
- · Frecuencia relativa acumulada(Hi): Es el resultado de sumar las
frecuencias relativas, tal y como explicamos para la frecuencia absoluta
acumulada.
- · Frecuencia absoluta(fi): Es la cantidad de observaciones que pertenecen a cada grupo. También, se interpreta como la cantidad de veces que se repite un suceso.
- · Frecuencia relativa(hi): Se calcula dividiendo la frecuencia absoluta entre el número de datos.
- · Frecuencia absoluta acumulada(Fi): Resulta de sumar las frecuencias
absolutas de una clase o grupo de la muestra (o población) con la anterior o
las anteriores.
- · Frecuencia relativa acumulada(Hi): Es el resultado de sumar las frecuencias relativas, tal y como explicamos para la frecuencia absoluta acumulada.
Ejemplificación:
Se le pidió a un grupo de personas que indiquen su color favorito, y se obtuvo los siguientes resultados:
Solución:
En la primera columna, colocamos los valores de nuestra variable, en la segunda la frecuencia absoluta, luego la frecuencia acumulada, seguida por la frecuencia relativa, y finalmente la frecuencia relativa acumulada. Por ser el primer problema, no haremos uso de las frecuencias porcentuales.
Argumento docente:
Las distribuciones de frecuencias son organizadores que facilitan al alumnado el proceso al momento de hacer un mejor análisis de los datos obtenidos de ciertos actividades, generadas para saber más sobre gustos o cantidades con base a lo que se obtuvo de distintos grupos.
Desde mi opinión deben de verse en grados como quinto o sexto, pues estos requieren de un mayor análisis de los datos y sobre todo algunas operaciones que requieren un mejor dominio de ellas o también un buen manejo de la calculadora para así poder estar todos en sintonía y que no se generen valores equivocados al momento de concluir.
En primaria, tienen una gran importancia pues en ese momento es en donde se enseña sobre el procedimiento para poder conocer los distintos tipos de frecuencias y que así en un futuro cuando sea necesario de ejecutar los puedan poner en práctica sin temor a equivocarse.
Ejercicio para aplicar en primaria:
Gráficas de barras Un gráfico de barras es una forma de
resumir un conjunto de datos por categorías. Muestra los datos usando varias
barras de la misma anchura, cada una de las cuales representa una categoría
concreta. La altura de cada barra es proporcional a una agregación específica
(por ejemplo, la suma de los valores de la categoría que representa). Las
categorías podrían ser desde grupos de edad a ubicaciones geográficas.
Características
-Una gráfica de barras tiene barras rectangulares con longitudes proporcionales a los valores que representan.
-Las gráficas de barras se utilizan para comparar dos o más valores.
-Las barras pueden ser horizontales o verticales.
-Los datos se representan con rectángulos de igual base sobre el eje de categorías (eje x o de abscisas); en tanto que la longitud del otro lado corresponde al valor del dato, según la escala utilizada en el eje de valores (eje y o de ordenadas).
-Cuando se representa más de una categoría existen diferentes tipos de presentación.
Normas generales de presentación:
- El ancho de la barra debe ser uniforme para todas las barras del diagrama.
- La longitud de la barra debe ser proporcional a la cantidad que representa.
- El espacio de separación entre barras por cada categoría debe ser constante.
- Las barras en estos gráficos pueden disponerse vertical u horizontalmente.
Las distribuciones de frecuencias son organizadores que facilitan al alumnado el proceso al momento de hacer un mejor análisis de los datos obtenidos de ciertos actividades, generadas para saber más sobre gustos o cantidades con base a lo que se obtuvo de distintos grupos.
Desde mi opinión deben de verse en grados como quinto o sexto, pues estos requieren de un mayor análisis de los datos y sobre todo algunas operaciones que requieren un mejor dominio de ellas o también un buen manejo de la calculadora para así poder estar todos en sintonía y que no se generen valores equivocados al momento de concluir.
En primaria, tienen una gran importancia pues en ese momento es en donde se enseña sobre el procedimiento para poder conocer los distintos tipos de frecuencias y que así en un futuro cuando sea necesario de ejecutar los puedan poner en práctica sin temor a equivocarse.
Ejercicio para aplicar en primaria:
Un gráfico de barras es una forma de resumir un conjunto de datos por categorías. Muestra los datos usando varias barras de la misma anchura, cada una de las cuales representa una categoría concreta. La altura de cada barra es proporcional a una agregación específica (por ejemplo, la suma de los valores de la categoría que representa). Las categorías podrían ser desde grupos de edad a ubicaciones geográficas.
Características
-Una gráfica de barras tiene barras rectangulares con longitudes proporcionales a los valores que representan.
-Las gráficas de barras se utilizan para comparar dos o más valores.
-Las barras pueden ser horizontales o verticales.
-Los datos se representan con rectángulos de igual base sobre el eje de categorías (eje x o de abscisas); en tanto que la longitud del otro lado corresponde al valor del dato, según la escala utilizada en el eje de valores (eje y o de ordenadas).
-Cuando se representa más de una categoría existen diferentes tipos de presentación.
Normas generales de presentación:
- El ancho de la barra debe ser uniforme para todas las barras del diagrama.
- La longitud de la barra debe ser proporcional a la cantidad que representa.
- El espacio de separación entre barras por cada categoría debe ser constante.
- Las barras en estos gráficos pueden disponerse vertical u horizontalmente.
Ejemplificación:
Argumento docente:
Las gráficas de barras son diagramas con las que podemos interpretar con mayor facilidad la información que queremos plasmar o analizar según lo necesitemos y para que sea visto e interpretada por otras personas.
Este tipo de organizadores son muy importantes de ver en primaria pues además de su facilidad de realización son muy prácticos de interpretar a pesar de las distintas variaciones que se pueden generar de este tipo, las cuales a pesar de eso no pierden su finalidad.
Como docentes es muy usual que los utilicemos, pues gracias a ellos podemos tomar mejores decisiones para actuar de mejor manera y así apoyar a nuestro alumnado en las áreas que mayormente se requiera o también para conocer más sobre sus preferencias personales.
Ejercicio para aplicar en primaria:
Diagramas de pastel Los diagramas de sectores (o de pastel) se usan a menudo para representar distribuciones de frecuencias de variables cualitativas. Se representa en un círculo cuyas proporciones (sectores circulares) tienen un área proporcional a las frecuencias absolutas de las modalidades de la variable.
Un gráfico
de pastel es un gráfico circular, el cual está dividido de tal manera que se
asemeja a las tajadas de un pastel. Este gráfico divide tus datos en sectores,
ilustrando cada proporción numérica con el fin de mostrar la composición como
un todo.
Las gráficas de barras son diagramas con las que podemos interpretar con mayor facilidad la información que queremos plasmar o analizar según lo necesitemos y para que sea visto e interpretada por otras personas.
Este tipo de organizadores son muy importantes de ver en primaria pues además de su facilidad de realización son muy prácticos de interpretar a pesar de las distintas variaciones que se pueden generar de este tipo, las cuales a pesar de eso no pierden su finalidad.
Como docentes es muy usual que los utilicemos, pues gracias a ellos podemos tomar mejores decisiones para actuar de mejor manera y así apoyar a nuestro alumnado en las áreas que mayormente se requiera o también para conocer más sobre sus preferencias personales.
Ejercicio para aplicar en primaria:
Los diagramas de sectores (o de pastel) se usan a menudo para representar distribuciones de frecuencias de variables cualitativas. Se representa en un círculo cuyas proporciones (sectores circulares) tienen un área proporcional a las frecuencias absolutas de las modalidades de la variable.
Un gráfico de pastel es un gráfico circular, el cual está dividido de tal manera que se asemeja a las tajadas de un pastel. Este gráfico divide tus datos en sectores, ilustrando cada proporción numérica con el fin de mostrar la composición como un todo.
Ejemplificación:
Argumento docente:
Los diagramas de pastel son herramientas interactivas que permiten interpretar la información de mejor manera con solo analizar el dibujo principal, pues siempre este representará el total de datos analizados y sus divisiones cada una de las características que se examinaron.
En la primaria, este tema es muy relevante pues a través de actividades que lo involucren podemos implicar a su vez aspectos de otras áreas de las matemáticas como podría ser el de figuras, ángulos, proporciones, entre otros, o del resto de las asignaturas como dibujo, colores, razonamiento, análisis, observación etcétera. Por lo tanto, a través de estos se pueden generar mayores aprendizajes que logran ser significativos y con un gran auge dentro de cualquier ámbito.
Ejercicio para aplicar en primaria:
¿Qué son?
Un histograma es una representación gráfica de una
variable en forma de barras, donde la superficie de cada barra es proporcional
a la frecuencia de los valores representados. En el eje vertical se representan
las frecuencias, y en el eje horizontal los valores de las variables,
normalmente señalando las marcas de clase, es decir, la mitad del intervalo en
el que están agrupados los datos.
Se utiliza
cuando se estudia una variable continua, como franjas de edades o altura de la
muestra, y, por comodidad, sus valores se agrupan en clases, es decir, valores
continuos. En los casos en los que los datos son cualitativos (no-numéricos),
como sexto grado de acuerdo o nivel de estudios, es preferible un diagrama de
sectores.
Los
histogramas son más frecuentes en ciencias sociales, humanas y económicas que
en ciencias naturales y exactas. Y permite la comparación de los resultados de
un proceso.
Ventajas
· - Su construcción ayudará a comprender la
tendencia central, dispersión y frecuencias relativas de los distintos valores.
· -Muestra grandes cantidades de datos ofreciendo
una visión clara y sencilla de su distribución.
Utilidades
· -Proporciona un punto de partida para formular
hipótesis acerca de un funcionamiento insatisfactorio.
· -Es especialmente útil
cuando se tiene un amplio número de datos que es preciso organizar, para
analizar más detalladamente o tomar decisiones sobre la base de ellos.
· -Es un medio eficaz para transmitir a
otras personas información sobre un proceso de forma precisa e inteligible.
· -Permite la comparación de los resultados
de un proceso con las especificaciones previamente establecidas para el mismo.
Ayuda a determinar si el proceso satisface los requisitos del cliente.
· - Hace posible determinar si ha habido
cambios en un proceso.
¿Cómo construir un histograma?
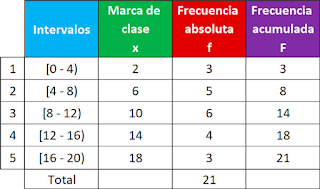
Partimos de una tabla de frecuencias con datos agrupados, y seguimos los siguientes pasos:
1. En el eje horizontal (X), colocamos los límites de
clase. Opcionalmente, puedes colocar las marcas de clase.
2. En el eje vertical (Y), colocamos las frecuencias. Se
suele tomar la frecuencia absoluta, pero también se puede trabajar con la
frecuencia relativa o con la frecuencia porcentual.
3. Dibujamos las barras de cada clase, teniendo en cuenta
que la altura de cada barra es igual a la frecuencia.
Ejemplificación:
Se registran los tiempos de las llamadas
recibidas en un call center, y se obtiene la siguiente tabla de frecuencias con
datos agrupados.
Solución:
Argumento docente:
Los histogramas son herramientas organizativas que ayudan al alumnado a generar un mayor análisis de los datos, en los que luego del proceso para obtenerlos les facilita una comprensión profunda de cada datos; por lo que de esa forma se puede interpretar para otros lo obtenido por medio de palabras.
En primaria estos temas deben de verse ya cuando se domine cada uno de los organizadores anteriores, pues de esa forma la técnica será mejor y no batallarán tanto en su realización; además que en este momento ya pueden elegir la herramienta que mayor beneficio les brinde para interpretar los datos y que así sea más fácil sus análisis e interpretación.
Ejercicio para aplicar en primaria:
Referencias de consulta:
-Disfruta las matemáticas. (s.f) Gráficas circulares (o
de pastel). Disponible en: http://www.disfrutalasmatematicas.com/datos/graficas-pastel.html
-EMatemáticas. (s.f). Representaciones gráficas. Disponible
en: https://www.ematematicas.net/graficas_estadistica.php?tipo=barras
-Formulas. (2019). Diagrama circular. Disponible en: https://www.universoformulas.com/estadistica/descriptiva/diagrama-circular/
-Guillermo Westreicher
(29 de abril, 2021). Distribución de frecuencias. Economipedia.com Disponible en: https://economipedia.com/definiciones/distribucion-de-frecuencias.html
-MateMovil.
(2019). Histogramas, ejemplos y
ejercicios. Disponible en: https://matemovil.com/histogramas-ejemplos-y-ejercicios/
-PlanCeibal.
(s.f). Histograma. Disponible en: https://rea.ceibal.edu.uy/elp/estad-stica/histograma.html
-SEP. (2020).
Libro de matemáticas de 1º a 6º.
-UNAM. (s.f.). GRÁFICA DE BARRAS. Disponible en: http://asesorias.cuautitlan2.unam.mx/Laboratoriovirtualdeestadistica/DOCUMENTOS/TEMA%201/6.%20GRAFICA%20DE%20BARRAS.pdf
-WebGid. (s.f). 3 Distribución de frecuencias. Disponible
en: https://www.uv.es/webgid/Descriptiva/3_distribucin_de_frecuencias.html